適用于直流激勵一階電路的三要素法
我們仍以簡單一階 RC 電路為出發點。 圖1 所示 RC 電路的全響應結果如下:

圖 1 一階RC電路圖
![]() ( 1 )
( 1 )
![]() ( 2 )
( 2 )
由 圖1 容易知道,電容電壓 ![]() 的初值為
的初值為 ![]() ,電容電壓的終值為
,電容電壓的終值為 ![]() ;而電流
;而電流 ![]() 的初值為
的初值為 ![]() ,電流
,電流 ![]() 的終值為
的終值為 ![]() 。
。
觀察式 ( 1 ) 、式 (2) 可見,一階電路中任意電路變量的全響應具有如下的統一形式:
![]() ( 3 )
( 3 )
可見,為求解一階電路中任一電路變量的全響應,我們僅須知道 三個要素 :電路變量的 初值 ![]() 、電路變量的 終值
、電路變量的 終值 ![]() 以及一階電路的 時間常數
以及一階電路的 時間常數 ![]() 。我們稱式 ( 6-5-3 ) 為一階電路分析的 三要素法 。三要素法同樣適用于一階 RL 電路,但是二階以上動態電路不可采用此法。
。我們稱式 ( 6-5-3 ) 為一階電路分析的 三要素法 。三要素法同樣適用于一階 RL 電路,但是二階以上動態電路不可采用此法。
推廣的三要素法
在前面分析一階電路時,我們采用的獨立源具有共同的特點,即所有獨立源均為直流(直流電壓源或直流電流源)。對于直流激勵電路,換路前電路變量為穩定的直流量,換路后經歷一個動態過程,電路變量過渡到另外一個穩定的直流量。我們容易根據電路的原始狀態和電路結構確定電路變量的 初值f(0+)、電路變量的 終值 f(∞)以及一階電路的 時間常數 ![]() 。如果電路中激勵源不是直流,而是符合一定變化規律的交流量(如正弦交流信號),則換路后電路經歷一個動態過程再次進入穩態,此時的穩態響應不再是直流形式,而依賴于激勵源的信號形式(如正弦交流信號)。此時,我們無法確定電路變量的 終值f(∞),故無法采用式 ( 3 ) “三要素法 ” 確定一階電路全響應。對于這類一階電路,我們可以采用推廣的三要素法:
。如果電路中激勵源不是直流,而是符合一定變化規律的交流量(如正弦交流信號),則換路后電路經歷一個動態過程再次進入穩態,此時的穩態響應不再是直流形式,而依賴于激勵源的信號形式(如正弦交流信號)。此時,我們無法確定電路變量的 終值f(∞),故無法采用式 ( 3 ) “三要素法 ” 確定一階電路全響應。對于這類一階電路,我們可以采用推廣的三要素法:
![]() 〔 4 )
〔 4 )
式中, ![]() 為全響應的 初值 、
為全響應的 初值 、 ![]() 為電路的 穩態響應 、τ為電路的 時間常數 ,稱為一階線性電路全響應的 三要素 ,
為電路的 穩態響應 、τ為電路的 時間常數 ,稱為一階線性電路全響應的 三要素 , ![]() 為全響應穩態解的初始值。
為全響應穩態解的初始值。
“三要素”的計算與應用
利用三要素法分析一階電路的全響應時,必須首先計算出電路變量的 初值![]() 、電路變量的 終值
、電路變量的 終值 ![]() 以及一階電路的 時間常數
以及一階電路的 時間常數 ![]() 。。假設激
。。假設激
勵源為直流電壓源或電流源。
• 初值 f(0+) 的計算
換路前,一般認為電路已進入穩態。根據電路結構以及元件屬性,我們不難確定動態元件的原始狀態(電容元件的電壓 ![]() 或電感元件的電流
或電感元件的電流 ![]() )。在有限激勵的作用下,電容元件的電壓或電感元件的電流不會發生突變。因此,在
)。在有限激勵的作用下,電容元件的電壓或電感元件的電流不會發生突變。因此,在 ![]() 時刻,電容元件的電壓
時刻,電容元件的電壓 ![]() 或電感元件的電流
或電感元件的電流 ![]() 維持原始狀態不變。我們可以用一個電壓源
維持原始狀態不變。我們可以用一個電壓源 ![]() 取代電容元件,或用一個電流源
取代電容元件,或用一個電流源 ![]() 取代電感元件。此時,電路被轉換成電阻電路,借助于電阻電路的支路分析法、回路分析法、結點分析法、戴維寧定理等即可計算出響應信號的初值
取代電感元件。此時,電路被轉換成電阻電路,借助于電阻電路的支路分析法、回路分析法、結點分析法、戴維寧定理等即可計算出響應信號的初值 ![]() 。
。
• 終值 f(∞)的計算
換路后,動態電路經過一個過渡過程,再次進入穩態。在直流激勵情況下, t=∞時,電容電壓和電感電流維持某個不變的取值。電容元件電流為 0 ,可以用開路元件取代,電感元件電壓為零,可以用短路元件取代。與初值計算相似,電路被轉換成電阻電路,借助于電阻電路的分析方法即可計算出響應信號的終值 f(∞)。
• 時間常數 τ的計算
實際的一階電路可能元件數量較大,結構較復雜,電路中包含多個電阻元件、獨立源、受控源和多個電容或電感。若電路滿足一階電路的條件,則其中的電容元件或電感元件之間必有強烈的相關性,表現在電路連接上為串聯、并聯或混聯關系。此時,換路后的電路模型可以看作由為某個電容網絡或電感網絡與一個含源電阻網絡相連組成,如圖2 ( a )所示。對電路中電容網絡或電感網絡進行串、并聯計算,得到一個等效電容 C eq 或一個等效電感Leq ,將含源電阻網絡進行諾頓等效或戴維寧等效,得到圖2 ( b )所示等效一階電路。則一階電路的時間常數τ 可計算如下:
![]() 或
或 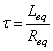 〔5 )
〔5 )
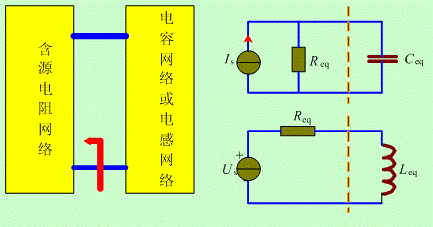
( a )電路模型分解 ( b )等效電路
圖2 一階電路的電路模型分解與等效


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底