一、電阻的Y形與△形聯接的概念
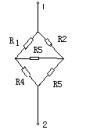
在電路中,有時電阻的聯結即非串聯又非并聯,如圖所示中,電阻![]() 的一端都接在一個公共結點上,各自的另一端則分別接到三個端子上,我們稱此聯結方式為Y形聯結;電阻
的一端都接在一個公共結點上,各自的另一端則分別接到三個端子上,我們稱此聯結方式為Y形聯結;電阻![]() 則分別接在三個端子的每兩個之間,我們稱之為三角形聯結。
則分別接在三個端子的每兩個之間,我們稱之為三角形聯結。
二、Y形和△形之間的等效變換


如圖所示,設它們對應端之間有相同電壓![]() 如果它們彼此等效,則
如果它們彼此等效,則
![]()
對于圖中![]() 聯結的電路,各電阻中的電流分別為
聯結的電路,各電阻中的電流分別為
![]()
![]()
![]()
對結點1、2、3分別列KCL方程,有
![]()
![]() (1)
(1)
![]()
而對圖![]() 聯結的電路,根據廣義回路分別列KVL方程,有
聯結的電路,根據廣義回路分別列KVL方程,有
![]()
![]()
又因 ![]()
求解上述三個方程,可得出
根據等效變換的原則,式(1)和式(2)中電壓![]() 、
、![]() 和
和![]() 前面的系數應該相應地相等,故經整理后可得
前面的系數應該相應地相等,故經整理后可得
![]()
![]() (3)
(3)
![]()
上式就是從已知的![]() 聯結電路的電阻來確定等效
聯結電路的電阻來確定等效 ![]() 電路的各對應電阻的關系式。
電路的各對應電阻的關系式。
也可整理成
![]()
![]() (4)
(4)
![]()
可見,上式就是從已知的![]() 聯結電路的電阻來確定等效
聯結電路的電阻來確定等效![]() 聯結電路的各對應電阻的關系式。
聯結電路的各對應電阻的關系式。
如果電路對稱,即當
![]()
![]()
則它們之間的變換關系為
![]()
![]()
關于電阻的![]() 和
和![]() 之間的等效變換,我們要認真理會其含義并加以記憶,在具體變換過程中,對各等效電阻應出現的位置不能搞錯。另外,由于電路圖的畫法可能不同,
之間的等效變換,我們要認真理會其含義并加以記憶,在具體變換過程中,對各等效電阻應出現的位置不能搞錯。另外,由于電路圖的畫法可能不同,![]() 和
和![]() 可畫成不同的形式,我們在使用時一定要仔細加以辨別。
可畫成不同的形式,我們在使用時一定要仔細加以辨別。
例題:求如圖所示中電路的等效電阻![]() ,其中R為3Ω。
,其中R為3Ω。
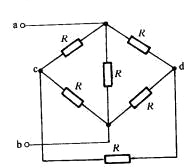
解:將聯結于結點C的三個電阻R作![]() 變換,各等效電阻
變換,各等效電阻![]() 為
為
![]()
變換后的電路如圖(b)所示。在圖(b)中
R與![]() 并聯等效電阻為
并聯等效電阻為![]()
所以 ![]()



 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底