描述結(jié)點(diǎn)處電流間的約束關(guān)系。
　　1.定律內(nèi)容：
　　在任一時(shí)刻，對(duì)任一結(jié)點(diǎn)，流入結(jié)點(diǎn)的電流之和恒等于流出該結(jié)點(diǎn)的電流之和。即
　　
　　如圖所示: 　　 　　對(duì)結(jié)點(diǎn)a：（注意首先要標(biāo)明參考方向）在結(jié)點(diǎn)a有三個(gè)電流與它關(guān)聯(lián)，根據(jù)KCL可寫出： 
　　對(duì)結(jié)點(diǎn)b：
　　對(duì)結(jié)點(diǎn)c：
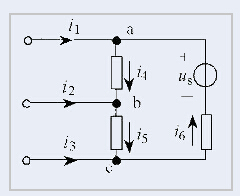
　　由結(jié)點(diǎn)a的KCL方程：
　　 
　　我們可以得到基爾霍夫電流定律的另一種描述：
　　對(duì)任一結(jié)點(diǎn)，結(jié)點(diǎn)電流代數(shù)和等于零，即。
　　注意：存在“＋－”號(hào)問題，若規(guī)定流入結(jié)點(diǎn)電流為＋，則流出為－；若規(guī)定流出為＋，則流入為－。
　　KCL實(shí)質(zhì)上反映了支路電流間的關(guān)系，揭示了在任一結(jié)點(diǎn)上電荷的守恒，即電荷在結(jié)點(diǎn)上既沒有消失，也沒有積累。
　　2.廣義KCL
　　KCL不僅適用于單個(gè)結(jié)點(diǎn)，也可推廣應(yīng)用于一個(gè)閉合面（又稱廣義結(jié)點(diǎn)）。
　　對(duì)圖中的虛線所示閉合面，共有3條支路與其相連，對(duì)應(yīng)的支路電流分別為，我們看其是否符合KCL定律。 　　 　　根據(jù)前面的分析我們得到了3個(gè)單個(gè)結(jié)點(diǎn)a，b，c的KCL方程，分別為：
　　結(jié)點(diǎn)a：    
　　結(jié)點(diǎn)b：    
　　結(jié)點(diǎn)c：    
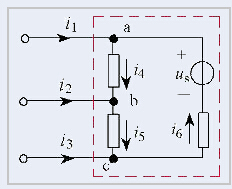
　　由上述3個(gè)方程，我們可以得出：
　　可見，對(duì)于圖中虛線所示的閉合面，如果把它看作一個(gè)結(jié)點(diǎn)（廣義結(jié)點(diǎn)），它也滿足KCL定律，和它相連的3條支路的支路電流的代數(shù)和為0。
　　描述：任一時(shí)刻，通過任意一個(gè)封閉面的電流的代數(shù)和等于零。
　　即：這個(gè)封閉面可以看成是一個(gè)廣義大結(jié)點(diǎn)，有。