邏輯函數(shù)表達(dá)式的標(biāo)準(zhǔn)形式有標(biāo)準(zhǔn)“與-或”表達(dá)式和標(biāo)準(zhǔn)“或-與”表達(dá)式兩種類型。兩種標(biāo)準(zhǔn)形式是建立在最小項(xiàng)和最大項(xiàng)概念的基礎(chǔ)之上的。
1.最小項(xiàng)和最大項(xiàng)
(1)最小項(xiàng)
定義:如果一個(gè)具有n個(gè)變量的函數(shù)的“與項(xiàng)”包含全部n個(gè)變量,每個(gè)變量都以原變量或反變量形式出現(xiàn)一次,且僅出現(xiàn)一次,則該“與項(xiàng)”被稱為最小項(xiàng)。有時(shí)又將最小項(xiàng)稱為標(biāo)準(zhǔn)“與”項(xiàng)。
數(shù)目:n個(gè)變量可以構(gòu)成2n個(gè)最小項(xiàng)。例如,3個(gè)變量A、B、C可以構(gòu)成![]() 、…、ABC共8個(gè)最小項(xiàng)。
、…、ABC共8個(gè)最小項(xiàng)。
簡(jiǎn)寫:通常用mi表示最小項(xiàng)。下標(biāo)i的取值規(guī)則是:按照變量順序?qū)⒆钚№?xiàng)中的原變量用1表示,反變量用0表示,由此得到一個(gè)二進(jìn)制數(shù),與該二進(jìn)制數(shù)對(duì)應(yīng)的十進(jìn)制數(shù)即下標(biāo)i的值。
例如,3變量A、B、C構(gòu)成的最小項(xiàng)![]() 可用m5表示。因?yàn)椤 ?
可用m5表示。因?yàn)椤 ?
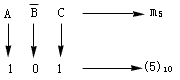
性質(zhì):最小項(xiàng)具有如下4條性質(zhì)。
性質(zhì)1: 任意一個(gè)最小項(xiàng),其相應(yīng)變量有且僅有一種取值使這個(gè)最小項(xiàng)的值為1。并且,最小項(xiàng)不同,使其值為1的變量取值不同。
性質(zhì)2:相同變量構(gòu)成的兩個(gè)不同最小項(xiàng)相“與”為0。因?yàn)槿魏我环N變量取值都不可能使兩個(gè)不同最小項(xiàng)同時(shí)為1,故相“與”為0。即
![]()
性質(zhì)3:n個(gè)變量的全部最小項(xiàng)相“或”為1。通常借用數(shù)學(xué)中的累加符號(hào)“Σ”,將其記為
![]()
這是因?yàn)閷?duì)于n個(gè)變量的任何一種取值,都有相應(yīng)的一個(gè)最小項(xiàng)為1,因此,全部最小項(xiàng)相或必為1。
性質(zhì)4:n個(gè)變量構(gòu)成的最小項(xiàng)有n個(gè)相鄰最小項(xiàng)。
相鄰最小項(xiàng)是指除一個(gè)變量互為相反外,其余部分均相同的最小項(xiàng)。例如 ,三變量最小項(xiàng)![]() 和ABC。
和ABC。
(2)最大項(xiàng)
定義:如果一個(gè)具有n個(gè)變量的函數(shù)的“或”項(xiàng)包含全部n個(gè)變量,每個(gè)變量都以原變量或反變量形式出現(xiàn)一次,且僅出現(xiàn)一次,則該“或”項(xiàng)被稱為最大項(xiàng)。有時(shí)又將最大項(xiàng)稱為標(biāo)準(zhǔn)“或”項(xiàng)。
數(shù)目:n個(gè)變量可以構(gòu)成2n 個(gè)最大項(xiàng)。例如,3個(gè)變量A、B、C可構(gòu)成A+B+C、![]() 共8個(gè)最大項(xiàng)。
共8個(gè)最大項(xiàng)。
簡(jiǎn)寫:通常用Mi表示最大項(xiàng)。下標(biāo)i的取值規(guī)則是:按照變量順序?qū)⒆畲箜?xiàng)中的原變量用0表示,反變量用1表示,由此得到一個(gè)二進(jìn)制數(shù),與該二進(jìn)制數(shù)對(duì)應(yīng)的十進(jìn)制數(shù)即下標(biāo)i的值。
例如,3個(gè)變量A、B、C構(gòu)成的最大項(xiàng)![]() 可用M5表示。因?yàn)?/FONT>
可用M5表示。因?yàn)?/FONT>
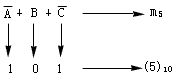
性質(zhì):最大項(xiàng)具有如下4條性質(zhì)。
性質(zhì)1:任意一個(gè)最大項(xiàng),其相應(yīng)變量有且僅有一種取值使這個(gè)最大項(xiàng)的值為0。并且,最大項(xiàng)不同,使其值為0的變量取值不同。
性質(zhì)2:相同變量構(gòu)成的兩個(gè)不同最大項(xiàng)相“或”為1。因?yàn)槿魏我环N變量取值都不可能使兩個(gè)不同最大項(xiàng)同時(shí)為0,故相“或”為1,即
![]()
性質(zhì)3:n個(gè)變量的全部最大項(xiàng)相“與”為0。通常借用數(shù)學(xué)中的累乘符號(hào)“Π”將其記為
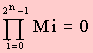
這是因?yàn)閷?duì)于n個(gè)變量的任何一種取值,都有相應(yīng)的一個(gè)最大項(xiàng)為0,因此,全部最大項(xiàng)相與必為0。
性質(zhì)4:n個(gè)變量構(gòu)成的最大項(xiàng)有n個(gè)相鄰最大項(xiàng)。相鄰最大項(xiàng)是指除一個(gè)變量互為相反外,其余變量均相同的最大項(xiàng)。
(3)最小項(xiàng)與最大項(xiàng)的關(guān)系
在同一問(wèn)題中下標(biāo)相同的最小項(xiàng)和最大項(xiàng)互為反函數(shù),或者說(shuō),相同變量構(gòu)成的最小項(xiàng)mi和最大項(xiàng)Mi之間存在互補(bǔ)關(guān)系。即
![]() 或
或 ![]()
2.邏輯函數(shù)表達(dá)式的標(biāo)準(zhǔn)形式
(1)標(biāo)準(zhǔn)與-或表達(dá)式
由若干最小項(xiàng)相“或”構(gòu)成的邏輯表達(dá)式稱為標(biāo)準(zhǔn)“與-或”表達(dá)式,也叫做最小項(xiàng)表達(dá)式。例如,![]() 是一個(gè)3變量函數(shù)的標(biāo)準(zhǔn)“與-或”表達(dá)式。 該函數(shù)表達(dá)式又可
是一個(gè)3變量函數(shù)的標(biāo)準(zhǔn)“與-或”表達(dá)式。 該函數(shù)表達(dá)式又可![]() 簡(jiǎn)寫為
簡(jiǎn)寫為
(2)標(biāo)準(zhǔn)或-與表達(dá)式
由若干最大項(xiàng)相“與”構(gòu)成的邏輯表達(dá)式稱為標(biāo)準(zhǔn)“或-與”表達(dá)式,也叫做最大項(xiàng)表達(dá)式 。例如,![]() 是一個(gè)3變量函數(shù)的標(biāo)準(zhǔn)“或-與”表達(dá)式。該表達(dá)式又可簡(jiǎn)寫為
是一個(gè)3變量函數(shù)的標(biāo)準(zhǔn)“或-與”表達(dá)式。該表達(dá)式又可簡(jiǎn)寫為
![]()


 返回頂部
返回頂部 刷新頁(yè)面
刷新頁(yè)面 下到頁(yè)底
下到頁(yè)底