邏輯函數的化簡就是使一個最初的邏輯函數經過化簡后得到式中的“與”項,“或”項項數最少,而每項中的變量數也最少。從而使組成的邏輯電路最簡(邏輯門數和每門的輸入端數最少)。
二、邏輯函數的代數法化簡
代數法是利用邏輯代數工具來達到使式子簡化的目的。化簡依據:邏輯代數定律、常用公式、和運算規則進行化簡。常用方法:有吸收法、配項法、合并法、消去法、 冗余法等。代數法化簡雖然簡單,但必須熟悉邏輯代數運算規則等,且具有一定的試探性,否則達不到最簡的目的。
三、邏輯函數的卡諾圖法化簡
1. 卡諾圖:用方格圖來描述邏輯函數,由于該方法由卡諾首先提出,所以把方格圖稱為卡諾圖。
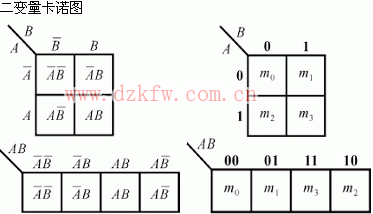
2. 如何畫卡諾圖:n個變量的函數,就有![]() 個小方格,一個小方格對應一個最小項,下面是2~5變量卡諾圖。
個小方格,一個小方格對應一個最小項,下面是2~5變量卡諾圖。
(a) 二變量A、B卡諾圖:![]() ,
,![]() 。
。
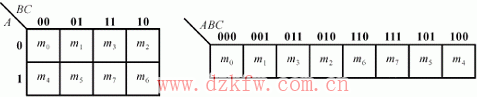
(b) 三變量A、B、C卡諾圖
三變量的八個最小項:![]() 。8個最小項在卡諾圖小方格上的位置必須以相鄰放置→相鄰方格中的最小項只差一個變量不同,其他相同。
。8個最小項在卡諾圖小方格上的位置必須以相鄰放置→相鄰方格中的最小項只差一個變量不同,其他相同。
(c) 四變量卡諾圖和五變量卡諾圖
3. 邏輯函數的卡諾圖表示
方法:首先將函數化成標準的“與—或”式,(最小項之和表達式),將式中最小項相應的小方格填“1”,式中沒有的最小項代表的小方格填“0”。填寫好后的圖形就是該函數的卡諾圖了。
4. 卡諾圖化簡的依據
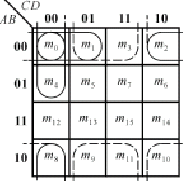 利用了相鄰二個小方格代表的最小項只差一個變量的相鄰性,它們可以合并成一項,消去一個變量的性質進行。下面用四變量卡諾圖為例加以說明。
利用了相鄰二個小方格代表的最小項只差一個變量的相鄰性,它們可以合并成一項,消去一個變量的性質進行。下面用四變量卡諾圖為例加以說明。
如:m0與m1結合(畫包圍圈),即:![]() 。
。
m0與m4結合(畫包圍圈),即:![]() 。
。
m1與m3結合(畫包圍圈),即:![]() 。
。
m0與m2結合(畫包圍圈),即:![]() 。
。
m1、m3、m9、m11結合,即:![]() 。
。
m0、m2、m8、m10結合,即:![]() 。
。
結論:包圍小方格結合最小項時,其結果是:消去包圍圈中不同的變量,保留相同的變量。
卡諾圖化簡時的一般原則和規律:
1. 只能對![]() 個相鄰方格實施包圍,包圍圈越大,式子越簡;
個相鄰方格實施包圍,包圍圈越大,式子越簡;
.2 . 小方格可以重復包圍,但每一包圍必須含有一個未被包圍過的方格,否則多余;
3. 包圍“1”格得原函數,包圍“0”格得反函數,經二次求反后分別可用“與非”邏輯和“或非”邏輯實現。
四、具有約束條件的邏輯函數的化簡
1.什么樣的邏輯函數稱為具有約束的邏輯函數?
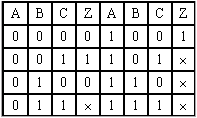 在許多邏輯問題中,邏輯變量與邏輯結果之間存在著某種限制、制約和約束的關系,如十字路口交通信號控制燈和汽車通行之間的關系。在任何時間,紅、綠、黃三只燈中只允許有一只燈亮,而不允許同時有二只或以上的燈亮,來控制指揮汽車通行、停止和準備。令燈暗為“0”,亮為“1”,車停為“1”,行為“0”。“×”為不允許出現(受制約的)燈亮組合,則有如下真值表。A-紅,B-綠,C-黃時真值表:從表看出:輸入變量的
在許多邏輯問題中,邏輯變量與邏輯結果之間存在著某種限制、制約和約束的關系,如十字路口交通信號控制燈和汽車通行之間的關系。在任何時間,紅、綠、黃三只燈中只允許有一只燈亮,而不允許同時有二只或以上的燈亮,來控制指揮汽車通行、停止和準備。令燈暗為“0”,亮為“1”,車停為“1”,行為“0”。“×”為不允許出現(受制約的)燈亮組合,則有如下真值表。A-紅,B-綠,C-黃時真值表:從表看出:輸入變量的![]() 組合是不允許出現的,是制約關系,這些項的取值與函數的結果無關。所以,這些項稱為無關項、約束項,或是任意項等。
組合是不允許出現的,是制約關系,這些項的取值與函數的結果無關。所以,這些項稱為無關項、約束項,或是任意項等。
2.具有約束條件的邏輯函數的表示方法
具有約束條件的邏輯函數,用最小項和約束項一起表示出來。
約束條件:![]()
或![]() 。
。
3.如何簡化具有約束的邏輯函數
由于約束項的存在與函數的結果無關,因此,在化簡時,約束項的取值可以當作“1”,也可以當作“0”處理,在卡諾圖中用符號“×”表示,以表示和其它最小項區別。



 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底