結(jié) 論：用3個節(jié)點電壓表示了6個支路電壓。進(jìn)一步減少了方程數(shù)。

1、節(jié)點電壓方程

根據(jù)KCL，可得圖3.2-1電路的節(jié)點電壓方程

 

節(jié)點電壓法分析電路的一般步驟
確定參考節(jié)點，并給其他獨立節(jié)點編號。列寫節(jié)點電壓方程，并求解方程，求得各節(jié)點電壓。由求得的節(jié)點電壓，再求其他的電路變量，如支路電流、電壓等。

例3.2-1 圖3.2-1所示電路中，G1=G2=G3=2S，G4=G5=G6=1S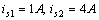， ，，求各支路電流。
解：1. 電路共有4個節(jié)點，選取d為參考點，。其他三個獨立節(jié)點的節(jié)點電壓分別為。
 

2. 列寫節(jié)點電壓方程
節(jié)點a：
節(jié)點b：
節(jié)點c：
代入?yún)��?shù)，并整理，得到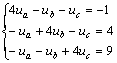

解方程，得

 

3. 求各支路電流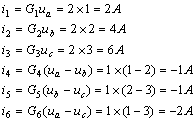

特 別 注 意：節(jié)點電壓方程的本質(zhì)是KCL，即Σ(流出電流) =Σ(流入電流)，在節(jié)點電壓方程中，方程的左邊是與節(jié)點相連的電導(dǎo)上流出的電流之和，方程的右邊則是與節(jié)點相連的電流源流入該節(jié)點的電流之和。如果某個電流源上還串聯(lián)有一個電導(dǎo)，那么該電導(dǎo)就不應(yīng)再計入自電導(dǎo)和互電導(dǎo)之中，因為該電導(dǎo)上的電流（與它串聯(lián)的電流源的電流）已經(jīng)計入方程右邊了。

例3.2-2 圖3.2-2所示電路，試列出它的節(jié)點電壓方程。

 解：對于節(jié)點a，流入的電流源的支路上還串聯(lián)了一個電阻R1，在計算a點的自電導(dǎo)時，不應(yīng)再把R1計算進(jìn)去，所以a點的節(jié)點電壓方程為

b點的節(jié)點電壓方程為

2、彌爾曼定理

當(dāng)電路只有兩個節(jié)點時，這種電路稱為單節(jié)偶電路（single node-pair circuit）。對于單節(jié)偶電路，有彌爾曼定理。
 

彌爾曼定理：對于只有兩個節(jié)點的單節(jié)偶電路，節(jié)偶電壓等于流入獨立節(jié)點的所有電流源電流的代數(shù)和除以節(jié)偶中所有電導(dǎo)之和。

二、含有電壓源的電路
 

1、有伴電壓源
結(jié) 論：如果電路中的電壓源是有伴電壓源，將有伴電壓源等效成有伴電流源。

方法一 把電壓源當(dāng)電流源處理
把電壓源當(dāng)作電流源看待，并設(shè)定電壓源的電流，列寫節(jié)點電壓方程。利用“電壓源的電壓等于其跨接的兩個獨立節(jié)點的節(jié)點電壓之差”這個關(guān)系，再補(bǔ)充一個方程式，聯(lián)立求解。

2、無伴電壓源
 

電壓源的一端與參考點相連

結(jié) 論
電壓源一端與參考點相連，另一端的節(jié)點電壓就是電壓源的電壓，節(jié)點電壓方程減少一個。

方法二 超節(jié)點（super node）方法
 

虛線框當(dāng)作一個超節(jié)點處理，列寫節(jié)點電壓方程。
注 意：列寫這個超節(jié)點的方程時，其中的“自電導(dǎo)×本節(jié)點電壓”這一項應(yīng)包括兩個部分，即組成該超節(jié)點的每個節(jié)點的電壓與其相應(yīng)的自電導(dǎo)的乘積。