例 2.2-1 電路如圖 2.2-1 所示, ![]() ,
, ![]() ,
, ![]() ,求各電阻兩端的電壓。
,求各電阻兩端的電壓。
解:圖中 R1 、 R2 、 R3 電阻相串聯,其等效電阻為
![]()
則 10A 電流源兩端的電壓
![]()
由分壓公式,得到
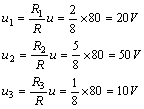
二、電阻的并聯( resistors in parallel )
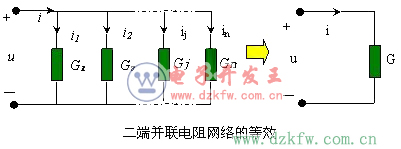
并 聯
n 個電導相并聯的二端網絡可用一個等效電導來等效,其等效電導 G 等于相并聯的各電導之和,即 ![]()
兩個電阻并聯時,其等效電阻為 ![]()
分流關系
對于并聯電阻網絡,電阻上分得的電流與其電導值成正比,即與其電阻值成反比。電阻值越大,其分得的電流越小。
第 j 個電導 ![]() 上分得的電流為
上分得的電流為
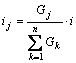
兩個電阻串聯時的分流公式為
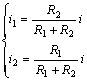
三、電阻的混聯
方 法
對于二端混聯電阻網絡的等效,關鍵是要抓住二端網絡的兩個端鈕,從一個端鈕出發,逐個元件地縷到另一個端鈕,分清每個部分的結構是串聯還是并聯,再利用串聯和并聯的等效公式,最終求得該二端混聯網絡的等效電路。
例 2.2-2 :求圖 2.2-2 ( a )所示電路 a 、 b 兩端的等效電阻 Rab 。

解:電路為多個電阻混聯,初一看似乎很復雜,但只要抓住端鈕 a 和 b ,從 a 點出發,逐點縷順,一直縷到另一端鈕 b 。為清楚起見,在圖 2.2-4 ( a )中標出節點 c 和 d 。就得到圖 2.2-4 ( b ),并可看出 5 Ω和 20 Ω的電阻是并聯,兩個 6 Ω的電阻也是并聯,其等效電阻分別是
![]()
![]()
這里,用符號“∥”表示兩個電阻的并聯關系。
由此,進一步得到圖 2.2-4 ( b )的等效電路圖 2.2-4 ( c )。再對 2.2-4 ( c )進行等效化簡,得到 2.2-4 ( d )。其中
![]()
所以 a 、 b 兩端的等效電阻
![]()


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底