帶電粒子在靜電場中的有很多種運動模式。常見的場強有:單個帶電粒子形成的場強(庫侖力),平行板電容器形成的勻強電場,無規(guī)則的場強(用電場線來描述的)。本文主要研究的是帶電粒子在勻強電場中的類平拋運動模式。
模型基本參量及圖像
一質(zhì)量為m,帶電量為q的正粒子從兩極板的中部以速度v0水平射入電壓為U的豎直向下的勻強電場中。
如圖所示,已知極板長度為L,極板間距離為d。存有兩種運動模式,一種是粒子能夠逃逸出電容,一種則落在電容器的下底板。
基本的物理量描述

(1)初始條件:帶電粒子有水平初速度v0;
(2)受力特點:帶電粒子受到豎直向下的恒定的電場力F=Eq;加速度
a=
(3)運動特點:水平方向為勻速直線運動,豎直方向為初速度為零的勻加速直線運動。與平拋運動相似,只不過加速度不為g,我們稱這樣的運動為類平拋運動。
(4)運動時間:若帶電粒子與極板不碰撞,在剛逃離電容器時,則運動時間為
 ;
;
若帶電粒子與極板碰撞,則運動時間可以從豎直方向求得
 ,故
,故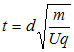
幾個特殊的物理量
(1)特征描述:側(cè)移(能逃離電容器的y軸偏轉(zhuǎn)量)

(2)能量特點:電場力做正功
 。
。
電場力做多少正功,粒子動能增加多少,電勢能就減少多少。
(3)重要結(jié)論:速度偏向角的正切:
 ,
,
位移偏向角的正切:
 ,
,
即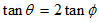 ,
,
即帶電粒子垂直進入勻強電場,它離開電場時,就好象是從初速度方向的位移中點沿直線射出來的。
例題與結(jié)論
如圖所示,質(zhì)量為m電荷量為q的帶電粒子以平行于極板的初速度v0射入長L板間距離為d的平行板電容器間,兩板間電壓為U,求射出時的側(cè)移、偏轉(zhuǎn)角和動能增量.
解:分解為兩個獨立的分運動:平行極板的勻速運動(運動時間由此分運動決定)
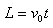 ,
,
垂直極板的勻加速直線運動
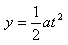 ,
,
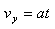 ,
,
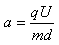 .
.
偏角:
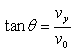 ,
,
得:
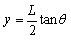 .
.
穿越電場過程的動能增量是:ΔEK=qEy (注意,一般來說不等于qU),
從例題可以得出結(jié)論:
結(jié)論一、不同帶電粒子從靜止進入同一電場加速后再垂直進入同一偏轉(zhuǎn)電場,射出時的偏轉(zhuǎn)角度總和位移偏轉(zhuǎn)量y是相同的,與粒子的q、m無關(guān)。
例1.如圖所示,電子在電勢差為U1的加速電場中由靜止開始運動,然后射入電勢差為U2的兩塊平行極板間的電場中,射入方向跟極板平行,整個裝置處在真空中,重力可忽略,在滿足電子能射出平行板區(qū)的條件下,下述四種情況中,一定能使電子的偏轉(zhuǎn)角θ變大的是( )
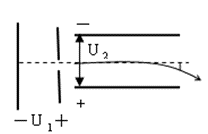
A.U1變大、U2變大B.U1變小、U2變大
C.U1變大、U2變小D.U1變小、U2變小
解析:電子在加速電場中由動能定理得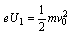 ,
,
電子在偏轉(zhuǎn)電場中有: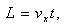
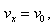
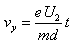 .
.
由以上各式得: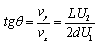 ,
,
可知要使θ增大必然U2變大,U1變小,故選B.答案:B
結(jié)論二、粒子垂直進入電場偏轉(zhuǎn)射出后,速度的反向延長線與初速度延長線的交點為粒子水平位移中點。(粒子好像是從中點直線射出!)
例2.證明:在帶電的平行金屬板電容器中,只要帶電粒子垂直電場方向射入(不一定在正中間),且能從電場中射出如圖所示,則粒子射入速度v0的方向與射出速度vt的方向的交點O必定在板長L的中點.
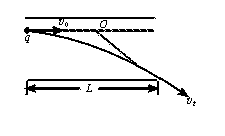
證明:粒子從偏轉(zhuǎn)電場中射出時偏距
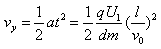 ,
,
粒子從偏轉(zhuǎn)電場中射出時的偏向角
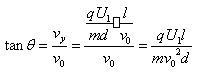 ,
,
作粒子速度的反向延長線,設(shè)交于O點,O點與電場邊緣的距離為x,則
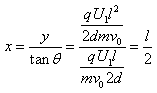 。
。
可知,粒子從偏轉(zhuǎn)電場中射出時,就好像是從極板間的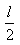 處沿直線射出似的,即證。
處沿直線射出似的,即證。
結(jié)論三、粒子垂直飛入電場偏轉(zhuǎn)射出時,速度偏轉(zhuǎn)角正切值(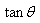 )等于位移偏轉(zhuǎn)角正切值(
)等于位移偏轉(zhuǎn)角正切值(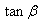 )的兩倍(
)的兩倍(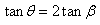 )。
)。
例3.(2009山東)如圖甲所示,建立Oxy坐標系,兩平行極板P、Q垂直于y軸且關(guān)于x軸對稱,極板長度和板間距均為l,第一四象限有磁場,方向垂直于Oxy平面向里。位于極板左側(cè)的粒子源沿x軸間右連接發(fā)射質(zhì)量為m、電量為+q、速度相同、重力不計的帶電粒子在0~3t時間內(nèi)兩板間加上如圖乙所示的電壓(不考慮極邊緣的影響)。已知t=0時刻進入兩板間的帶電粒子恰好在t0時,刻經(jīng)極板邊緣射入磁場。上述m、q、l、l0、B為已知量。(不考慮粒子間相互影響及返回板間的情況)
(1)求電壓U的大小。
(2)求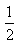 時進入兩板間的帶電粒子在磁場中做圓周運動的半徑。
時進入兩板間的帶電粒子在磁場中做圓周運動的半徑。
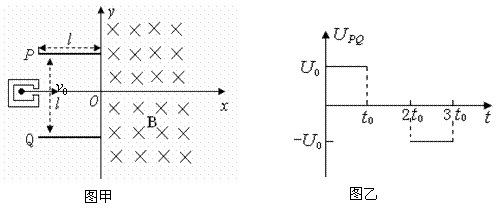
解析:(1)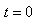 時刻進入兩極板的帶電粒子在電場中做勻變速曲線運動,
時刻進入兩極板的帶電粒子在電場中做勻變速曲線運動,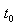 時刻剛好從極板邊緣射出,在y軸負方向偏移的距離為
時刻剛好從極板邊緣射出,在y軸負方向偏移的距離為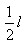 ,
,
則有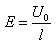 ,
,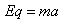 ,
,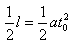 聯(lián)立以上三式,解得兩極板間偏轉(zhuǎn)電壓為
聯(lián)立以上三式,解得兩極板間偏轉(zhuǎn)電壓為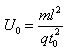 。
。

(2)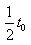 時刻進入兩極板的帶電粒子,前
時刻進入兩極板的帶電粒子,前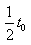 時間在電場中偏轉(zhuǎn),后
時間在電場中偏轉(zhuǎn),后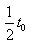 時間兩極板沒有電場,帶電粒子做勻速直線運動。帶電粒子沿x軸方向的分速度大小為
時間兩極板沒有電場,帶電粒子做勻速直線運動。帶電粒子沿x軸方向的分速度大小為
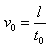 ,帶電粒子離開電場時沿y軸負方向的分速度大小為
,帶電粒子離開電場時沿y軸負方向的分速度大小為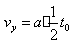 ,帶電粒子離開電場時的速度大小為
,帶電粒子離開電場時的速度大小為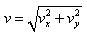 ,設(shè)帶電粒子離開電場進入磁場做勻速圓周運動的半徑為R,
,設(shè)帶電粒子離開電場進入磁場做勻速圓周運動的半徑為R,
則有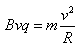 ,
,
聯(lián)立上式解得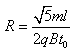 。
。
本題是高考物理真題,考查的是帶電粒子在勻強電場、勻強磁場中的運動。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底