通過任意一個閉合曲面的電通量等于包圍在該閉合面內所有電荷電量的代數和除以
這個閉合面習慣上叫高斯面。閉合面內的電荷可能有正有負,電量的代數和指的是正負電荷電量的代數和。
2、高斯定理的證明
(1)單個點電荷包圍在同心球面內 
設空間有一點電荷![]() ,其周圍激發電場。以
,其周圍激發電場。以![]() 為球心,
為球心,![]() 為半徑作一球面
為半徑作一球面![]() 為高斯面。則高斯面上各點場強的大小相等,方向沿矢徑方向向外。在高斯面上取一面元
為高斯面。則高斯面上各點場強的大小相等,方向沿矢徑方向向外。在高斯面上取一面元![]() ,則通過
,則通過![]() 的電通量為
的電通量為
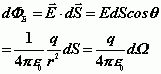
通過整個高斯面的電通量為![]()
(2)單個點電荷包圍在任意閉合曲面內
在閉合曲面![]() 內以
內以![]() 為球心,
為球心,![]() 為半徑作一任意球面
為半徑作一任意球面![]() 為高斯面。在
為高斯面。在![]() 面上取一面元
面上取一面元 ![]() ,則通過
,則通過![]() 的電通量為
的電通量為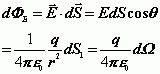
通過整個閉合曲面![]() 的電通量為
的電通量為![]()

以
即![]() 和
和![]() 的數值相等,符號相反,它們的代數和為零。而通過整個閉合曲面的電通量
的數值相等,符號相反,它們的代數和為零。而通過整個閉合曲面的電通量 ![]() 是通過這樣一對對面元的電通量之和,因而也等于零。
是通過這樣一對對面元的電通量之和,因而也等于零。
(4)多個點電荷的情形 
設空間同時存在![]() 個點電荷,其中
個點電荷,其中![]() 在高斯面 之內,
在高斯面 之內,![]() 在高斯面
在高斯面![]() 之外。設
之外。設![]() 面上任一點的場強為
面上任一點的場強為![]() ,由場強疊加原理,得
,由場強疊加原理,得
![]()
式中![]() 是各點電荷單獨存在時的場強。穿過 面的電通量為
是各點電荷單獨存在時的場強。穿過 面的電通量為
高斯定理是靜電場的兩條基本定理之一,它反映了靜電場的基本性質:靜電場是有源場,"源"即電荷。此外高斯定理不僅對靜電場適用,對變化的電場也適用,它是電磁場理論的基本方程之一。
Tags:高斯定理,定義
責任編輯:admin


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底