1、緒論
這篇文章是機械臂專欄的第一期,該文章旨在對機械臂基礎知識進行簡要的概述,為之后機械臂的運動學和動力學仿真做好鋪墊。該篇文章只進行整體的知識架構(gòu)梳理和具體知識的簡要介紹,并不會過多深入,其中內(nèi)容主要來源與John J. Craig 的著名著作《機器人學導論》,請需要學習機械臂的同學無比熟讀該書。
首先介紹一下我將要介紹的主要知識點,空間描述與轉(zhuǎn)換、機械臂運動學、機械臂速度與靜力。
為什么要學習空間描述與轉(zhuǎn)換呢,我們可以看下圖,機械臂是若干個桿連接而形成的(連接兩個桿的地方是關節(jié)),而在機械臂中這些桿稱為連桿,每個連桿可以在夫連桿(上一連桿)的基礎上繞某一軸旋轉(zhuǎn),(關節(jié)通過電機旋轉(zhuǎn)帶動連桿旋轉(zhuǎn)),而這個軸只與夫連桿相對禁止,這就導致一旦多個連桿都進行運動時,連桿只能與“上一級連桿”和“下一級連桿”進行直接的空間轉(zhuǎn)換關系,也就是說當我知道第一個連桿旋轉(zhuǎn)的角度時,我就能根據(jù)底座的空間坐標推算出第一個連桿的具體位置,然后一級一級往后推就能獲得最末端機械臂的位置,也就是接卸比末端位置。而空間描述和轉(zhuǎn)換就是學習如何一級一級計算空間坐標,也就是學習從固定的底座開始,空間時如何通過連桿旋轉(zhuǎn)一步一步轉(zhuǎn)換的。
機械臂運動學就很好理解了,面對機械臂,我們肯定是研究如何使得機械臂按照我們意愿去運動,如何控制機械臂末端的位置。比如用機械臂拿杯子,肯先要控制末端到達杯子位置,所以這里就設計到運動學知識,分為正運動學和逆運動學,正運動學就是已知每個關節(jié)電機的旋轉(zhuǎn)角度,推算出末端工具的空間位姿(這里的位姿其實就是空間位置加上空間朝向)。逆運動學就是已知我末端空間位置,推算出各個關節(jié)的角度,這就類似于拿杯子,我知道杯子位置,需要推算出末端工具到達該位置需要每個關節(jié)旋轉(zhuǎn)多大角度。
機械臂速度與靜力,就涉及到動力學知識,首先學習機械臂速度,是為了描述每個連桿線速度和角速度是如何傳遞的,其中比較主要的知識點就是雅可比矩陣,該矩陣描述了每個關節(jié)速度與末端的位姿速度。而機械臂靜力就涉及到機械臂動力學知識,主要講的是機械臂在某個姿態(tài)各關節(jié)以速度、加速度運動時,關節(jié)電機需要輸出的力矩,如果末端對外界施加力,這里還需要加入施加力反作用在各個關節(jié)的力矩。
2、空間位置、姿態(tài)與位姿的描述
2.1,位置表示
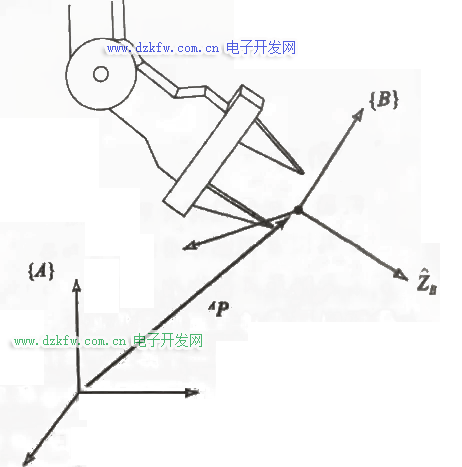
當我們對機械臂建立坐標系時,往往將底座作為基準坐標系,圖中坐標系A便是基準坐標系,就能用一個3\times1的位置矢量給出坐標系中的任何點定位。還要注意矢量定義在哪一個坐標系。^AP是指相對坐標系A的一個點的位置。
世界坐標系中的任何點都可以用一個3×1的位置矢量進行定位,例如:
2.2、位姿表示
不僅需要表示空間中的點的位位置,還需要描述物體的姿態(tài),也就是該點出物體的方向。上圖確定了操作臂末端位置,若姿態(tài)也確定,末端的位姿就能完全被確定下來。為了描述物體的姿態(tài),我們在物體上固定一個坐標系并且給出此坐標系相對于參考坐標系的描述。如下圖的參考系B即為固定在物體上的。
用XB,YB,ZB來表示坐標系{B}各主軸方向的單位矢量,當用坐標系{A}來表示時,它們被寫成AXB,AYB,AZB,將三個單位矢量按AXB,AYB,AZB順序排列組成一個3×3的矩陣,稱之為旋轉(zhuǎn)矩陣,用符號ABR來表示。
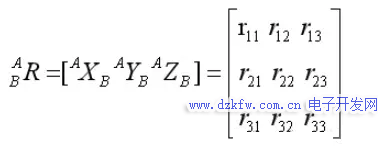
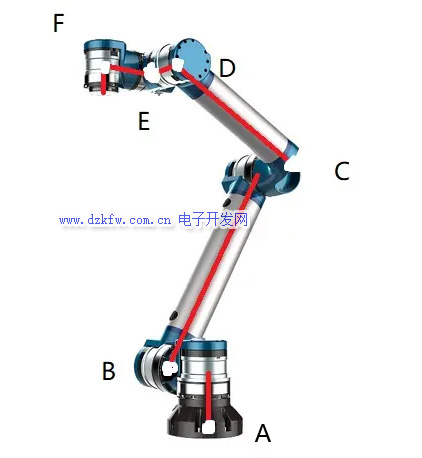
有了位姿的描述,我們就能知道一個連桿末端也就是關節(jié)相對于上一關節(jié)的位姿,依次描述最后就能獲得末端位姿。如圖所示,紅色表示連桿,白色表示關節(jié)處,每個關節(jié)處就代表一個坐標系,通過坐標系的遞推計算,就能算出末端坐標系相對基準坐標系的位姿。
接下來就時如何計算坐標系的位姿。
2.3 坐標系平移
可以從圖中看出,B坐標系就是相對A坐標系進行平移
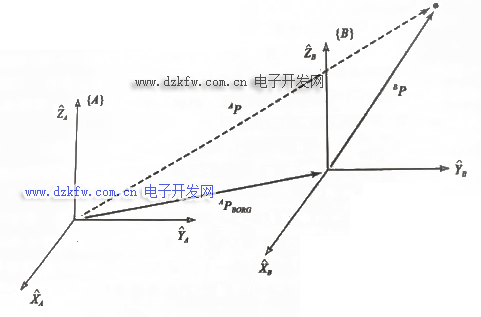
此時,我們用矢量相加的辦法求點P相對于A的表示^AP:
2.4 坐標系旋轉(zhuǎn)

若我們已知矢量相對于B的定義^BP,現(xiàn)在想求矢量相對于A的定義,且兩個坐標系原點重合,我們已知^A_BR,那么我們是可以求解的。
該式可簡化為旋轉(zhuǎn)矩陣形式表示:
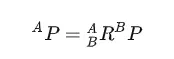
有了矩坐標系的偏移和旋轉(zhuǎn),我們就可以根據(jù)基準坐標系推算出連接連桿的坐標系。

如圖所示為兩個坐標系有相對的偏移和旋轉(zhuǎn),于是就有:

而這樣表示兩個坐標系的關系就顯得很麻煩,于是通過定義轉(zhuǎn)換算子來方便描述:
于是我們就可以通過轉(zhuǎn)換算子來描述兩個坐標系的關系,同樣轉(zhuǎn)換算子是可以疊加的,通過不斷的疊加就可以算出末端與基準坐標系的轉(zhuǎn)換算子,也就是得到末端相對于基準坐標系的位姿。
3 、機械臂運動學
3.1、連桿表示
首先學習機械臂運動學,就需要了解機械臂的結(jié)構(gòu),連桿與連桿之間的坐標系是如何變換的,是如何平移,如何旋轉(zhuǎn),使得某一連桿坐標系按照這個平移旋轉(zhuǎn)之后能夠獲得下一個連桿的坐標系,也即是兩個連桿之間的坐標系算子與連桿結(jié)構(gòu)的關系,更直白的意思就是,如果知道某一關節(jié)的角度,就能找到關節(jié)連接的兩個連桿坐標系對于的變換算子T。
常見的操作臂的結(jié)構(gòu)一般優(yōu)先選擇只有一個自由度的關節(jié)作為連桿的連接方式,大部分的操作臂中會包括轉(zhuǎn)動關節(jié)和移動關節(jié)。只有很少見的情況,會使用具有n個自由度的關節(jié),這種關節(jié)也可以抽象的看做用n個單自由度的關節(jié)與n-1個長度的連桿組合而成的。
我們在討論操作臂時,會從固定基座開始為連桿編號,我們習慣性地成固定基座為連桿0,接下來的第一個能動的連桿被稱為連桿1,以此類推,最末端的的連桿就稱為連桿n

上圖就是一種連桿描述方式,用四個參數(shù)描述兩個連桿的相對位姿關系:

也就是如上分析,知道兩個連桿的具體相對位姿關系后,就能推算出兩個連桿坐標系的轉(zhuǎn)換算子T:
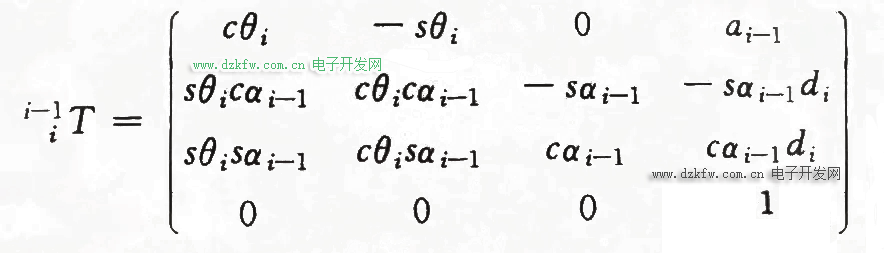
這樣,只要我知道每個連桿相對關系,就能推算出機械臂末端相對基準坐標的轉(zhuǎn)換算子,也就是能夠得到末端相對基準坐標系的位置和狀態(tài)。
3.2、運動學原理
在這個連桿關系中,有一個參數(shù)θ,他是動態(tài)變化的,就是其他三個參數(shù)是不會變化,而該參數(shù)θ就是關節(jié)旋轉(zhuǎn)角度,所以我們就能根據(jù)每個關節(jié)旋轉(zhuǎn)角度推算出機械臂末端相對基準坐標系的變換算子,從而得到機械臂末端的位姿,這就是正運動學。
當我們知道末端位姿時,希望機械臂能達到該位置,就首先推算處該變換算子關于θ的公式:

然后有已知的基準坐標系位姿和末端位姿進行矩陣運算的具體參數(shù) T,然后進行方程求解,但是逆運動學的求解難度會隨著機械臂關節(jié)數(shù)量的變換成幾何倍增。
大概的運動學知識點就講解到這里,有關動力學知識會在之后動力學仿真部分講解,而接下來將會發(fā)布運動學的各種仿真方法。







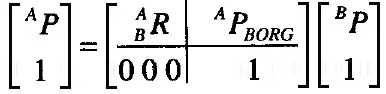

 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底