AVO、Rid對運算電路的影響
前面討論的基本運算電路中,將集成運放看成理想的,而實際的集成運放并非如此。因此,實際工作情況與理想化分析所得的結論之間必然存在誤差,即產生了運算誤差。
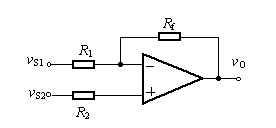
圖 1 差分輸入電路
集成運放的Avd和Rid為有限值時,對運算電路將引起誤差,現以圖1所示的運算放大電路為例來討論,用圖2電路來等效,
由此可列出如下方程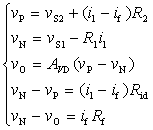
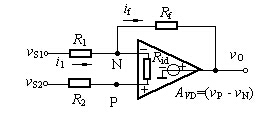
圖2 Avd、Rid產生運算誤差電路
解之可得
其中 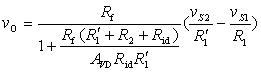
![]()
當vS2=0,圖1即為反相比例運算電路。為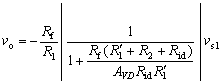
通常用AVDRidR1>>Rf(R1+R2+Rid),利用近似公式(|x|<<1時![]() )上式可化簡為
)上式可化簡為 ![]()
閉環電壓增益 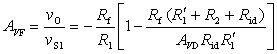
反相比例運算電路的理想閉環增益為 ![]()
由此可得相對誤差 ![]()
![]()
上式說明,AVD和Rid越大,AVF越接近理想值,產生的誤差也越小。按類似方法可以分析同相比例運算電路。
共模抑制比KCMR對運算電路的影響
以同相運算放大電路為例,集成運放的共模抑制比KCMR為有限時,對運算電路引起的誤差近似為![]()
由此可見,AVD和KCMR越大,誤差越小,AVF越接近理想情況下的值。
誤差推導過程
由圖1的電路有
差模輸入電壓為 ![]()
共模輸入電壓為 ![]()
運算放大電路總的輸出電壓為
理想情況下,![]() ,由此求得相對誤差
,由此求得相對誤差
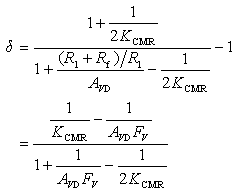
式中![]() 為電壓反饋系數。通常
為電壓反饋系數。通常![]() ,
,![]() ,
,
因此上式簡化為
輸入失調電壓、輸入失調電流對運算電路的影響
輸入失調電壓VIO、輸入失調電流IIO不為零時,運算電路的輸出電壓將產生誤差。根據VIO和IIO的定義,將運放用圖1來等效,其中小三角符號內代表理想運放。
利用戴維南定理和諾頓定理可將兩輸入端化簡,如圖2所示,則![]()
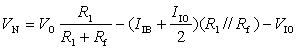
因為![]() ,有
,有![]() ,則由上兩式求出
,則由上兩式求出
由于電路中兩輸入端均接地,在VIO、IIB和IIO作用下,產生的輸出電壓VO即是絕對誤差。
若R2=R1//Rf,由IIB引起的誤差可以消除,輸出電壓變為![]()
由上式可見,![]() 和R2越大,VIO和IIO引起的輸出誤差電壓也越大。
和R2越大,VIO和IIO引起的輸出誤差電壓也越大。
當用作積分運算時,因電容C代替Rf,輸出誤差電壓為
則 ![]()
由上式可見,積分時間常數t=R1C越小或積分時間越長,誤差越大。減小誤差的辦法是選用失調及溫漂小的高精度、超高精度運放,或將時間常數適應選大些。也可以在輸入級加調零電位器或在輸入端加一補償電壓或補償電流,以抵消VIO和IIO的影響,使vO(t)為零。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底