世界上第一臺計算機

認真讀了之前一篇科普文章的讀者會問：“為什么計算機的CPU主要由邏輯門組成？”恭喜你，這說明你不僅“學”而且“思”了。邏輯門可以搭建邏輯電路，完成推理和判斷。但計算機更重要的能力還是計算。如果邏輯門不能完成計算，其作用就有限了。那么邏輯門能完成計算嗎？

從三角函數到微積分的所有計算，歸根到底都可以分解為“加、減、乘、除”計算，而它們又可以歸結為“加法”計算。因為減法等于加上負數，乘法等于多次加法，除法等于多次減法。因此，只要邏輯門可以構成“加法器”，理論上就可以完成所有計算。

邏輯門構成加法器的關鍵，就是大名鼎鼎的二進制。早在1679年，偉大的數學家萊布尼茲就發明了二進制。就憑這一項發明，萊布尼茲對科學的貢獻度就應該不在牛頓之下。

我們日常熟悉的十進制有九個符號：0、1、2、3、4、5、6、7、8、9，逢10進1。二進制只有兩個符號：0、1，逢2進1。圖1是二進制與十進制對照表。

圖1 二進制

從圖中可以看出，只要記住逢2進1，二進制的加法計算與我們熟悉的十進制是相同的，而且更加簡潔。采用一些簡單的數學技巧，二進制數與十進制數可以相互換算。

圖2是4位二進制數的加法運算：

圖2 二進制加法運算

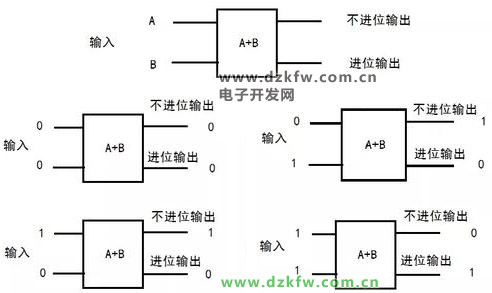
從圖2可以分解出二進制加法的2個環節：

相加不進位

相加進位

圖3 二進制相加分解

圖中右下角就是記0進1的意思。

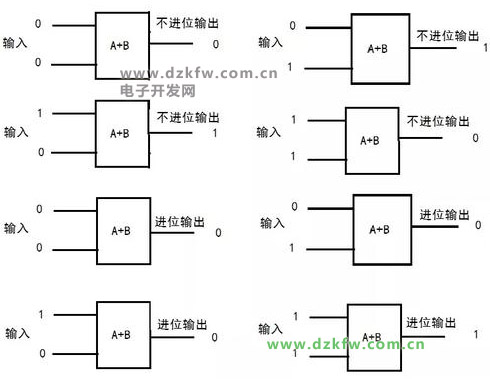
從圖3可以看出，進位與不進位輸出正好是2種邏輯門，如圖4所示：

圖4 與二進制等價的2種邏輯門

圖中的進位輸出恰好就是與（AND）門。而不進位輸出可以用圖5的被稱為“異或門”的邏輯門構成：

圖5 不進位輸出邏輯門：異或門

用或門、與非門、與門構成圖5左下角的邏輯電路，稱為異或（XOR）門。有興趣的讀者不妨用A=0 ，A=1，B=0，B=1輸入邏輯門，仔細運算驗證，其輸入輸出關系恰好就是二進制加法的不進位輸出。

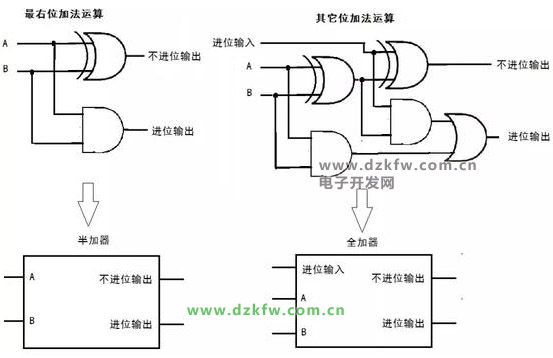
現在我們可以用邏輯門來完成圖二進制加法，如圖6。

圖6 半加器、全加器

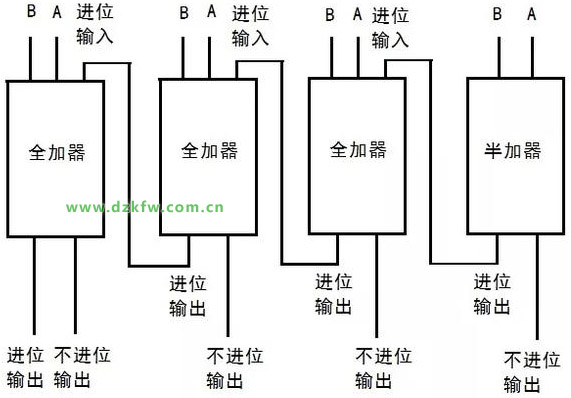
任意多少位的二進制加法器都可以用圖6所示的半加器、全加器構成，如圖7。

圖7 用半加器、全加器構成的加法器

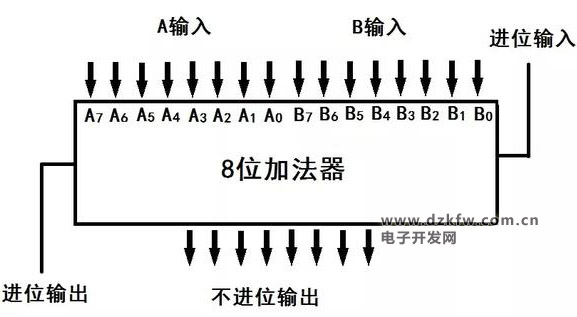
圖7是加法器的原理示意圖，將其輸入輸出重新排列，就可以得到通常的加法器原理圖，如圖8所示。

圖8 8位加法器原理圖

用2個8位加法器串聯就可以構成16位加法器。至此，我們就清楚了邏輯門構成加法器的原理，從而也就理解了邏輯門完成計算的基本原理。但是請讀者們務必注意，以上的描述只是邏輯門完成計算的基本原理，實際過程要復雜許多。