數(shù)據(jù)結(jié)構(gòu)和算法是相輔相成的。數(shù)據(jù)結(jié)構(gòu)是為算法服務(wù)的,算法要作用在特定的數(shù)據(jù)結(jié)構(gòu)之上。 因此,我們無(wú)法孤立數(shù)據(jù)結(jié)構(gòu)來(lái)講算法,也無(wú)法孤立算法來(lái)講數(shù)據(jù)結(jié)構(gòu)。
比如,因?yàn)閿?shù)組具有隨機(jī)訪問(wèn)的特點(diǎn),常用的二分查找算法需要用數(shù)組來(lái)存儲(chǔ)數(shù)據(jù)。但如果我們選擇鏈表這種數(shù)據(jù)結(jié)構(gòu),二分查找算法就無(wú)法工作了,因?yàn)殒湵聿⒉恢С蛛S機(jī)訪問(wèn)。
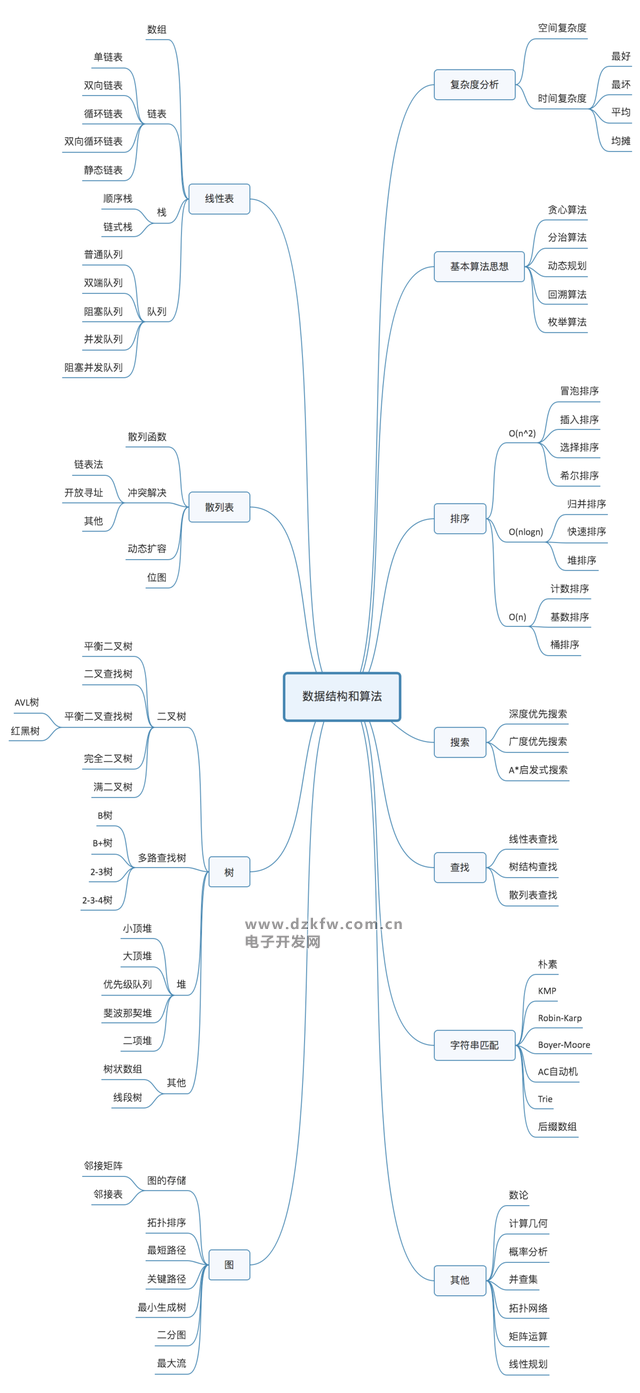
10 個(gè)數(shù)據(jù)結(jié)構(gòu):數(shù)組、鏈表、棧、隊(duì)列、散列表、二叉樹、堆、跳表、圖、Trie 樹;
10 個(gè)算法:遞歸、排序、二分查找、搜索、哈希算法、貪心算法、分治算法、回溯算法、動(dòng)態(tài)規(guī)劃、字符串匹配算法。
要學(xué)習(xí)它的“來(lái)歷”“自身的特點(diǎn)”“適合解決的問(wèn)題”以及“實(shí)際的應(yīng)用場(chǎng)景”。
千萬(wàn)不要被動(dòng)地記憶,要多辯證地思考,多問(wèn)為什么。
一些可以讓你事半功倍的學(xué)習(xí)技巧:
-
邊學(xué)邊練,適度刷題
-
多問(wèn)、多思考、多互動(dòng)
-
-
知識(shí)需要沉淀,不要想試圖一下子掌握所有
學(xué)習(xí)的過(guò)程中,我們碰到最大的問(wèn)題就是,堅(jiān)持不下來(lái)。
我們?cè)诳菰锏膶W(xué)習(xí)過(guò)程中,也可以給自己設(shè)立一個(gè)切實(shí)可行的目標(biāo),就像打怪升級(jí)一樣。
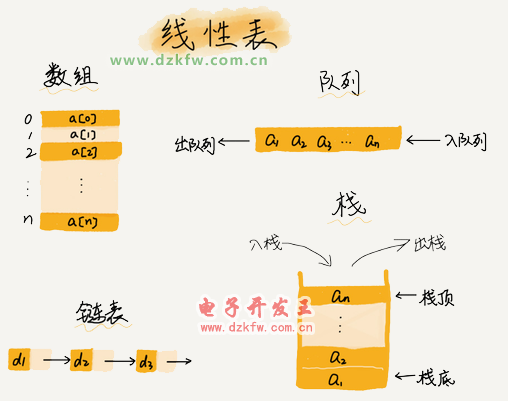
1、數(shù)組
2、鏈表
緩存的大小有限,當(dāng)緩存被用滿時(shí),哪些數(shù)據(jù)應(yīng)該被清理出去,哪些數(shù)據(jù)應(yīng)該被保留?這就需要緩存淘汰策略來(lái)決定。常見的策略有三種:先進(jìn)先出策略 FIFO(First In,F(xiàn)irst Out)、最少使用策略 LFU(Least Frequently Used)、最近最少使用策略 LRU(Least Recently Used)。
三種最常見的鏈表結(jié)構(gòu),它們分別是:單鏈表、雙向鏈表和循環(huán)鏈表。
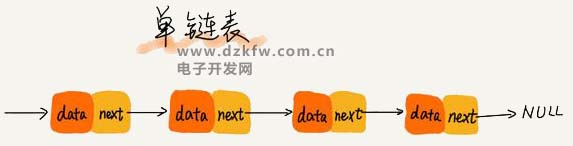
(1)單鏈表
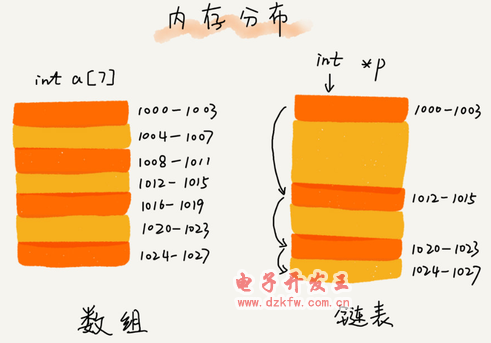
鏈表通過(guò)指針將一組零散的內(nèi)存塊串聯(lián)在一起。其中,我們把內(nèi)存塊稱為鏈表的“結(jié)點(diǎn)”。為了將所有的節(jié)點(diǎn)串起來(lái),每個(gè)鏈表的結(jié)點(diǎn)除了存儲(chǔ)數(shù)據(jù)之外,還需要記錄鏈上的下一個(gè)節(jié)點(diǎn)的地址。如圖所示,我們把這個(gè)記錄下個(gè)結(jié)點(diǎn)地址的指針叫作后繼指針 next。
從我畫的單鏈表圖中,你應(yīng)該可以發(fā)現(xiàn),其中有兩個(gè)結(jié)點(diǎn)是比較特殊的,它們分別是第一個(gè)結(jié)點(diǎn)和最后一個(gè)結(jié)點(diǎn)。我們習(xí)慣性地把第一個(gè)結(jié)點(diǎn)叫作頭結(jié)點(diǎn),把最后一個(gè)結(jié)點(diǎn)叫作尾結(jié)點(diǎn)。其中,頭結(jié)點(diǎn)用來(lái)記錄鏈表的基地址。有了它,我們就可以遍歷得到整條鏈表。而尾結(jié)點(diǎn)特殊的地方是:指針不是指向下一個(gè)節(jié)點(diǎn),而是指向一個(gè)空地址 NULL,表示這是鏈表上最后一個(gè)節(jié)點(diǎn)。
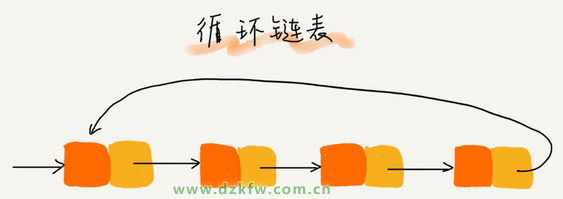
(2)循環(huán)鏈表
當(dāng)要處理的數(shù)據(jù)具有環(huán)型結(jié)構(gòu)特點(diǎn)時(shí),就特別適合采用循環(huán)鏈表。比如著名的約瑟夫問(wèn)題。
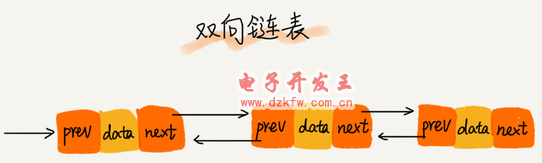
(3)雙向鏈表
雙向鏈表需要額外的兩個(gè)空間來(lái)存儲(chǔ)后繼結(jié)點(diǎn)和前驅(qū)結(jié)點(diǎn)的地址。所以,如果存儲(chǔ)同樣多的數(shù)據(jù),雙向鏈表要比單鏈表占用更多的內(nèi)存空間。雖然兩個(gè)指針比較浪費(fèi)存儲(chǔ)空間,但可以支持雙向遍歷,這樣也帶來(lái)了雙向鏈表操作的靈活性。
雙向鏈表可以支持 O(1) 時(shí)間復(fù)雜度的情況下找到前驅(qū)結(jié)點(diǎn)。
所以數(shù)組適合做查詢,比如查詢算法都是用數(shù)組,鏈表適合做儲(chǔ)存,比如lru會(huì)考慮鏈表。
如何輕松寫出正確的鏈表代碼?
還記得如何表示一個(gè)空鏈表嗎?head=null 表示鏈表中沒(méi)有結(jié)點(diǎn)了。其中 head 表示頭結(jié)點(diǎn)指針,指向鏈表中的第一個(gè)節(jié)點(diǎn)。
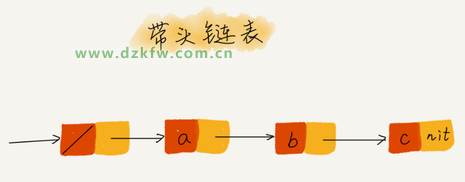
如果我們引入哨兵結(jié)點(diǎn),在任何時(shí)候,不管鏈表是不是空,head 指針都會(huì)一直指向這個(gè)哨兵結(jié)點(diǎn)。我們也把這種有哨兵結(jié)點(diǎn)的鏈表叫帶頭鏈表。相反,沒(méi)有哨兵結(jié)點(diǎn)的鏈表就叫作不帶頭鏈表。
哨兵結(jié)點(diǎn)是不存儲(chǔ)數(shù)據(jù)的。因?yàn)樯诒Y(jié)點(diǎn)一直存在,所以插入第一個(gè)結(jié)點(diǎn)和插入其他結(jié)點(diǎn),刪除最后一個(gè)節(jié)點(diǎn)和刪除其他結(jié)點(diǎn),都可以統(tǒng)一為相同的代碼實(shí)現(xiàn)邏輯了。
3、棧
當(dāng)某個(gè)數(shù)據(jù)集合只涉及在一端插入和刪除數(shù)據(jù),并且滿足后進(jìn)先出、先進(jìn)后出的特性,我們就應(yīng)該首選“棧”這種數(shù)據(jù)結(jié)構(gòu)。
比較經(jīng)典的一個(gè)應(yīng)用場(chǎng)景就是1、 函數(shù)調(diào)用棧.2、棧在表達(dá)式求值中的應(yīng)用3、棧在括號(hào)匹配中的應(yīng)用
leetcode上關(guān)于棧的題目大家可以先做20,155,232,844,224,682,496.
4、隊(duì)列
循環(huán)隊(duì)列
循環(huán)隊(duì)列,顧名思義,它長(zhǎng)得像一個(gè)環(huán)。原本數(shù)組是有頭有尾的,是一條直線。現(xiàn)在我們把首尾相連,扳成了一個(gè)環(huán)。
阻塞隊(duì)列
阻塞隊(duì)列其實(shí)就是在隊(duì)列基礎(chǔ)上增加了阻塞操作。簡(jiǎn)單來(lái)說(shuō),就是在隊(duì)列為空的時(shí)候,從隊(duì)頭取數(shù)據(jù)會(huì)被阻塞。因?yàn)榇藭r(shí)還沒(méi)有數(shù)據(jù)可取,直到隊(duì)列中有了數(shù)據(jù)才能返回;如果隊(duì)列已經(jīng)滿了,那么插入數(shù)據(jù)的操作就會(huì)被阻塞,直到隊(duì)列中有空閑位置后再插入數(shù)據(jù),然后再返回。
并發(fā)隊(duì)列
線程安全的隊(duì)列我們叫作并發(fā)隊(duì)列。最簡(jiǎn)單直接的實(shí)現(xiàn)方式是直接在 enqueue()、dequeue() 方法上加鎖,但是鎖粒度大并發(fā)度會(huì)比較低,同一時(shí)刻僅允許一個(gè)存或者取操作。
5、跳表
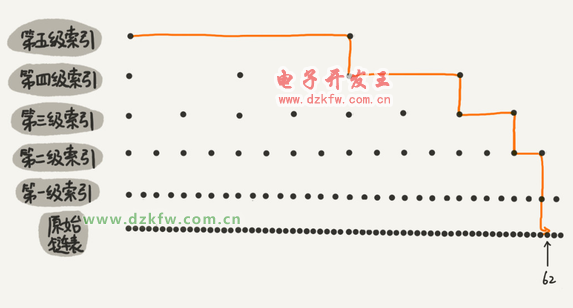
這種鏈表加多級(jí)索引的結(jié)構(gòu),就是跳表。
用跳表查詢到底有多快?
第 k 級(jí)索引的結(jié)點(diǎn)個(gè)數(shù)是第 k-1 級(jí)索引的結(jié)點(diǎn)個(gè)數(shù)的 1/2,那第 k級(jí)索引結(jié)點(diǎn)的個(gè)數(shù)就是 n/(2k)。
時(shí)間復(fù)雜度: O(m*logn)。
跳表是不是很浪費(fèi)內(nèi)存?
跳表需要存儲(chǔ)多級(jí)索引,肯定要消耗更多的存儲(chǔ)空間。
跳表的空間復(fù)雜度是 O(n)。
為什么 Redis 要用跳表來(lái)實(shí)現(xiàn)有序集合,而不是紅黑樹?
Redis 中的有序集合支持的核心操作主要有下面這幾個(gè):
-
插入一個(gè)數(shù)據(jù);
-
刪除一個(gè)數(shù)據(jù);
-
查找一個(gè)數(shù)據(jù);
-
按照區(qū)間查找數(shù)據(jù)(比如查找值在 [100, 356] 之間的數(shù)據(jù));
-
迭代輸出有序序列。
其中,插入、刪除、查找以及迭代輸出有序序列這幾個(gè)操作,紅黑樹也可以完成,時(shí)間復(fù)雜度跟跳表是一樣的。但是,按照區(qū)間來(lái)查找數(shù)據(jù)這個(gè)操作,紅黑樹的效率沒(méi)有跳表高。
對(duì)于按照區(qū)間查找數(shù)據(jù)這個(gè)操作,跳表可以做到 O(logn) 的時(shí)間復(fù)雜度定位區(qū)間的起點(diǎn),然后在原始鏈表中順序往后遍歷就可以了。這樣做非常高效。
還有,跳表更加靈活,它可以通過(guò)改變索引構(gòu)建策略,有效平衡執(zhí)行效率和內(nèi)存消耗。
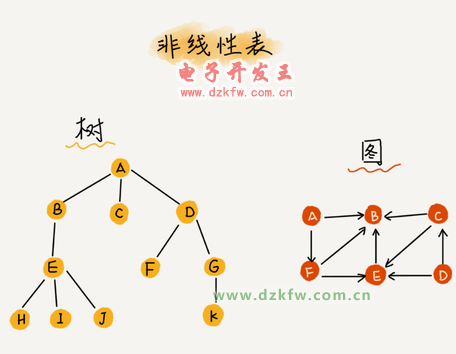
6、二叉樹
7、Trie樹(字典樹)
Trie 樹,也叫“字典樹”。顧名思義,它是一個(gè)樹形結(jié)構(gòu)。它是一種專門處理字符串匹配的數(shù)據(jù)結(jié)構(gòu),用來(lái)解決在一組字符串集合中快速查找某個(gè)字符串的問(wèn)題。
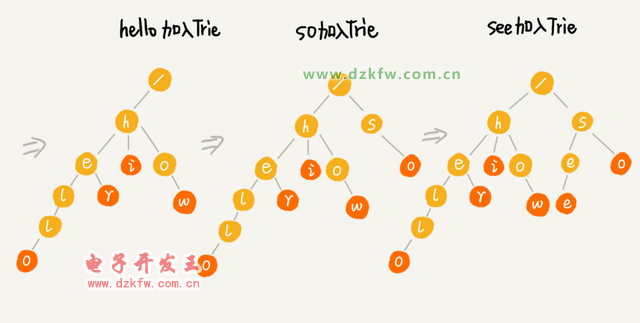
Trie 樹主要有兩個(gè)操作
-
一個(gè)是將字符串集合構(gòu)造成 Trie 樹,就是一個(gè)將字符串插入到 Trie 樹的過(guò)程。
-
另一個(gè)是在 Trie 樹中查詢一個(gè)字符串。
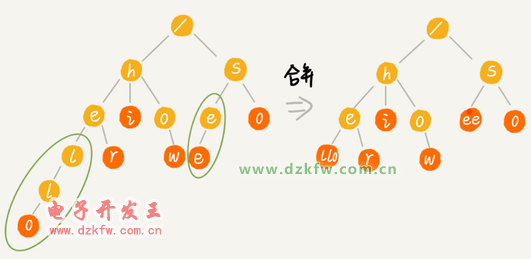
Trie 樹的變體有很多,都可以在一定程度上解決內(nèi)存消耗的問(wèn)題。比如,縮點(diǎn)優(yōu)化
在一組字符串中查找字符串,Trie 樹實(shí)際上表現(xiàn)得并不好。它對(duì)要處理的字符串有及其嚴(yán)苛的要求。
-
第一,字符串中包含的字符集不能太大。我們前面講到,如果字符集太大,那存儲(chǔ)空間可能就會(huì)浪費(fèi)很多。即便可以優(yōu)化,但也要付出犧牲查詢、插入效率的代價(jià)。
-
第二,要求字符串的前綴重合比較多,不然空間消耗會(huì)變大很多。
-
第三,如果要用 Trie 樹解決問(wèn)題,那我們就要自己從零開始實(shí)現(xiàn)一個(gè) Trie 樹,還要保證沒(méi)有 bug,這個(gè)在工程上是將簡(jiǎn)單問(wèn)題復(fù)雜化,除非必須,一般不建議這樣做。
-
第四,我們知道,通過(guò)指針串起來(lái)的數(shù)據(jù)塊是不連續(xù)的,而 Trie 樹中用到了指針,所以,對(duì)緩存并不友好,性能上會(huì)打個(gè)折扣。
綜合這幾點(diǎn),針對(duì)在一組字符串中查找字符串的問(wèn)題,我們?cè)诠こ讨校鼉A向于用散列表或者紅黑樹。因?yàn)檫@兩種數(shù)據(jù)結(jié)構(gòu),我們都不需要自己去實(shí)現(xiàn),直接利用編程語(yǔ)言中提供的現(xiàn)成類庫(kù)就行了。
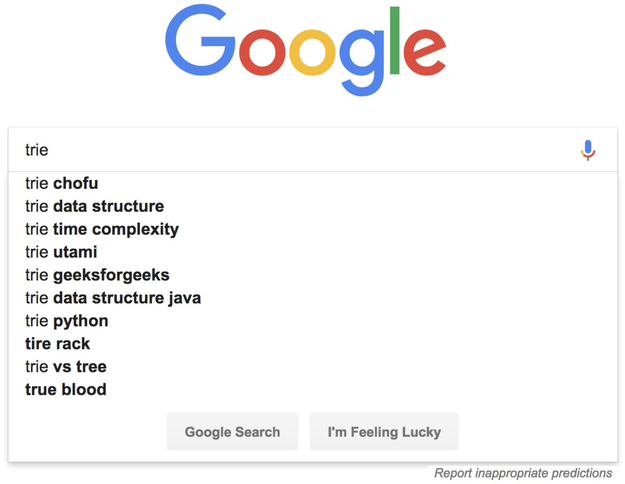
實(shí)際上,Trie 樹只是不適合精確匹配查找,這種問(wèn)題更適合用散列表或者紅黑樹來(lái)解決。Trie 樹比較適合的是查找前綴匹配的字符串,也就是類似開篇問(wèn)題的那種場(chǎng)景。
8、散列表(Hash Table)
散列表(哈希表)用的是數(shù)組支持按照下標(biāo)隨機(jī)訪問(wèn)數(shù)據(jù)的特性,所以散列表其實(shí)就是數(shù)組的一種擴(kuò)展,由數(shù)組演化而來(lái)。可以說(shuō),如果沒(méi)有數(shù)組,就沒(méi)有散列表。
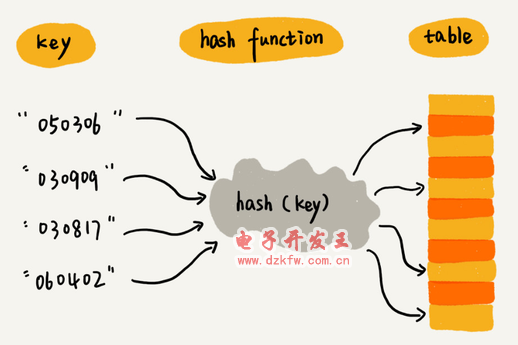
一般有key和value,key會(huì)通過(guò)散列函數(shù)轉(zhuǎn)換成散列值
散列函數(shù)(哈希函數(shù))
散列表兩個(gè)核心問(wèn)題是散列函數(shù)設(shè)計(jì)和散列沖突解決。
散列函數(shù)設(shè)計(jì)的基本要求:
-
散列函數(shù)計(jì)算得到的散列值是一個(gè)非負(fù)整數(shù);
-
如果 key1 = key2,那 hash(key1) == hash(key2);
-
如果 key1 ≠ key2,那 hash(key1) ≠ hash(key2)。
第一二點(diǎn)沒(méi)啥問(wèn)題,但第三點(diǎn)理解起來(lái)可能會(huì)有問(wèn)題,要想找到一個(gè)不同的 key 對(duì)應(yīng)的散列值都不一樣的散列函數(shù),幾乎是不可能的。即便像業(yè)界著名的MD5、SHA、CRC等哈希算法,也無(wú)法完全避免這種散列沖突。而且,因?yàn)閿?shù)組的存儲(chǔ)空間有限,也會(huì)加大散列沖突的概率。
我們常用的散列沖突解決方法有兩類,開放尋址法和鏈表法。
1. 開放尋址法
開放尋址法的核心思想是,如果出現(xiàn)了散列沖突,我們就重新探測(cè)一個(gè)空閑位置,將其插入。
-
線性探測(cè):如果存儲(chǔ)位置已經(jīng)被占用了,我們就從當(dāng)前位置開始,依次往后查找,看是否有空閑位置,直到找到為止。
-
二次探測(cè):跟線性探測(cè)很像,線性探測(cè)每次探測(cè)的步長(zhǎng)是 1,那它探測(cè)的下標(biāo)序列就是 hash(key)+0,hash(key)+1,hash(key)+2……而二次探測(cè)探測(cè)的步長(zhǎng)就變成了原來(lái)的“二次方”,也就是說(shuō),它探測(cè)的下標(biāo)序列就是 hash(key)+0,hash(key)+12,hash(key)+22……
-
雙重散列:意思就是不僅要使用一個(gè)散列函數(shù)。我們使用一組散列函數(shù) hash1(key),hash2(key),hash3(key)……我們先用第一個(gè)散列函數(shù),如果計(jì)算得到的存儲(chǔ)位置已經(jīng)被占用,再用第二個(gè)散列函數(shù),依次類推,直到找到空閑的存儲(chǔ)位置。
當(dāng)數(shù)據(jù)量比較小、裝載因子小的時(shí)候,適合采用開放尋址法。這也是 Java 中的ThreadLocalMap使用開放尋址法解決散列沖突的原因。
2. 鏈表法
所有散列值相同的元素我們都放到相同槽位對(duì)應(yīng)的鏈表中。
為什么HashMap使用鏈表法解決哈希沖突
1、首先,鏈表法對(duì)內(nèi)存的利用率比開放尋址法要高。因?yàn)殒湵斫Y(jié)點(diǎn)可以在需要的時(shí)候再創(chuàng)建,并不需要像開放尋址法那樣事先申請(qǐng)好。實(shí)際上,這一點(diǎn)也是我們前面講過(guò)的鏈表優(yōu)于數(shù)組的地方。
2、鏈表法比起開放尋址法,對(duì)大裝載因子的容忍度更高。開放尋址法只能適用裝載因子小于 1 的情況。接近 1 時(shí),就可能會(huì)有大量的散列沖突,導(dǎo)致大量的探測(cè)、再散列等,性能會(huì)下降很多。但是對(duì)于鏈表法來(lái)說(shuō),只要散列函數(shù)的值隨機(jī)均勻,即便裝載因子變成 10,也就是鏈表的長(zhǎng)度變長(zhǎng)了而已,雖然查找效率有所下降,但是比起順序查找還是快很多。




 返回頂部
返回頂部 刷新頁(yè)面
刷新頁(yè)面 下到頁(yè)底
下到頁(yè)底